مشكلة عالم الرياضيات في العصور الوسطى ليوناردو فيبوناتشي حول الأرانب

دعونا نرى كيف ينمو عدد الأرانب في الأشهر الستة الأولى:

الشهر 1. زوج واحد من الأرانب الصغيرة.

الشهر 2. لا يزال هناك زوج أصلي واحد. الأرانب لم تبلغ سن الإنجاب بعد.

الشهر 3. زوجان: الأصل الذي بلغ سن الإنجاب + زوج من الأرانب الصغيرة التي أنجبتها.

الشهر 4. ثلاثة أزواج: زوج أصلي واحد + زوج أرانب واحد أنجبته في بداية الشهر + زوج أرانب ولدت في الشهر الثالث ولكنها لم تصل بعد إلى مرحلة النضج الجنسي.

الشهر الخامس. خمسة أزواج: زوج أصلي واحد + زوج ولد في الشهر الثالث وبلغ سن الإنجاب + زوجان جديدان الأزواج الذين أنجبوا + زوج واحد ولدا في الشهر الرابع ولكن لم يصلوا بعد النضج.

الشهر 6. ثمانية أزواج: خمسة أزواج من الشهر الماضي + ثلاثة أزواج حديثي الولادة. إلخ.

لتوضيح الأمر ، دعنا نكتب البيانات المستلمة في الجدول:

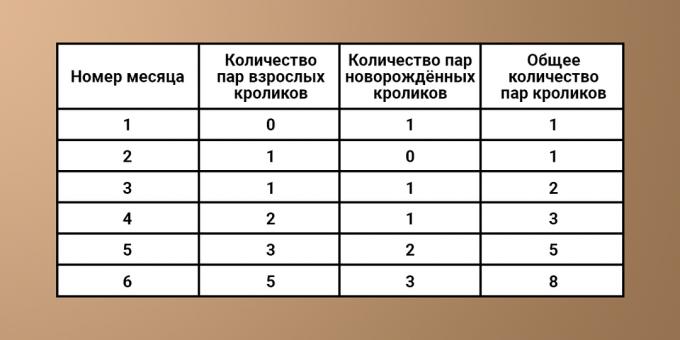
إذا قمت بفحص الجدول بعناية ، يمكنك تحديد النمط التالي. في كل مرة يكون عدد الأرانب الموجودة في الشهر التاسع مساويًا لعدد الأرانب في (ن - 1) الشهر السابق ، مع تلخيصها بعدد الأرانب المولودة حديثًا. عددهم ، بدوره ، يساوي العدد الإجمالي للحيوانات اعتبارًا من الشهر (n - 2) (الذي كان قبل شهرين). من هنا يمكنك أن تستنتج معادلة:

F_ن = F._{ن - 1}+ ف_{ن - 2},

حيث F_ن - إجمالي عدد أزواج الأرانب في الشهر التاسع ، و_{ن - 1} هو إجمالي عدد أزواج الأرانب في الشهر السابق ، و F_{ن - 2} - العدد الإجمالي لأزواج الأرانب قبل شهرين.

دعونا نحسب عدد الحيوانات في الأشهر التالية باستخدامه:

الشهر 7. 8 + 5 = 13.

الشهر الثامن. 13 + 8 = 21.

الشهر 9. 21 + 13 = 34.

الشهر العاشر. 34 +21 = 55.

الشهر 11. 55 + 34 = 89.

الشهر 12. 89 + 55 = 144.

الشهر 13 (بداية العام المقبل). 144 + 89 = 233.

في بداية الشهر الثالث عشر ، أي في نهاية العام ، سيكون لدينا 233 زوجًا من الأرانب. ومن بين هؤلاء ، سيكون 144 زوجًا من البالغين و 89 من الشباب. التسلسل الناتج 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 تسمى أرقام فيبوناتشي. في ذلك ، كل رقم نهائي جديد يساوي مجموع السابقتين.