الإحماء للدماغ: هل يمكنك حل مشكلة العملات المزيفة؟ تحقق من ذلك!

لدى عالم الرياضيات ثلاث محاولات فقط ، لذا لا يمكنك وزن كل عملة على حدة. تحتاج إلى تقسيمهم إلى أكوام ووضعهم على الميزان عدة قطع في كل مرة ، والاقتراب تدريجيًا من المقياس المزيف.

لنفترض أن عالم رياضيات قرر تقسيم 12 قطعة نقدية إلى ثلاثة أكوام من أربع عملات لكل منها. ثم وضع أربع عملات معدنية على كل مقياس. يمكن أن يؤدي هذا الوزن إلى نتيجتين. دعونا نفكر في كل منهم.

1. كان وزن كومة العملات المعدنية هو نفسه. لذلك ، فإن كل الأموال الموجودة فيها حقيقية ، والمزيف يقع في مكان ما بين العملات المعدنية الأربع غير الموزونة.

لتتبع النتيجة ، يضع عالم الرياضيات علامة على جميع البرامج النصية بصفر. ثم أخذ ثلاثة منهم وقارنهم بثلاث عملات غير موزونة. إذا كان وزنهما متساويًا ، تكون العملة المتبقية (الرابعة) غير الموزونة مزورة. إذا كان الوزن مختلفًا ، يضع عالم الرياضيات زائدًا على العملات المعدنية الثلاثة غير المميزة إذا كانت أثقل من تلك التي تحتوي على أصفار ، أو ناقص إذا كانت أخف.

ثم يأخذ اثنين عملات معدنيةتم وضع علامة زائد أو ناقص ويقارن وزنهم. إذا كانت هي نفسها ، فإن النسخة المتبقية مزيفة. إذا لم يكن الأمر كذلك ، ينظر عالم الرياضيات إلى العلامات: من بين العملات ذات علامة الجمع ، سيكون المزيف هو الأثقل ، من بين العملات ذات علامة السالب ، العملة الأفتح.

2. لم يكن وزن كومة العملات المعدنية هو نفسه.

في هذه الحالة ، يحتاج عالم الرياضيات إلى التصرف على النحو التالي: وضع علامة على النقود في كومة ثقيلة بعلامة موجب ، في كومة خفيفة مع سالب ، في كومة غير موزونة بصفر ، حيث أنه من المعروف أن النسخة المزيفة كانت على الميزان.

أنت الآن بحاجة إلى إعادة تجميع العملات المعدنية لتحتفظ بالوزن المتبقيين. تتمثل إحدى الطرق في أخذ ثلاث عملات مع علامة موجب ، بدلاً من ثلاث عملات ناقص ، ووضع ثلاث قطع بصفر في مكانها.

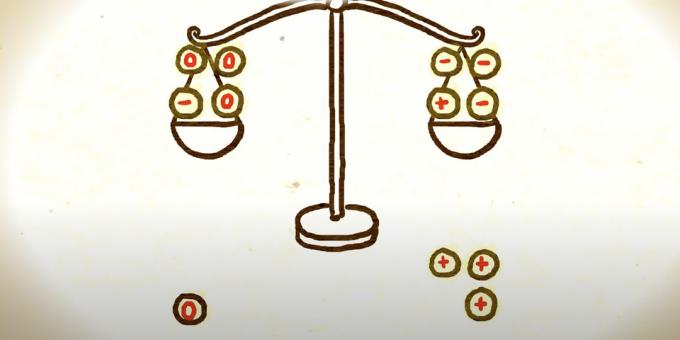
تتبع ثلاثة خيارات ممكنة. إذا كان المقياس الذي كان أثقل لا يزال يفوق وزنه ، فإما أن تكون العملة القديمة التي عليها علامة الجمع أثقل من العملات الأخرى ، أو تكون العملة ذات علامة الطرح على الجانب الآخر من الميزان أفتح. يحتاج عالم الرياضيات إلى اختيار أي منها ومقارنتها بنمط شائع للعثور على مزيف.

إذا أصبح كفة الميزان ، التي كانت أثقل وزنًا ، أخف وزناً ، فإن واحدة من العملات المعدنية الثلاث التي تحمل علامة الطرح التي يحركها عالم الرياضيات هي الأخف وزناً. الآن يحتاج إلى مقارنة اثنين منهم على الميزان. إذا تم ربط النتائج ، فإن العملة الثالثة ستكون مزيفة. في حالة عدم المساواة ، يكون المزيف أسهل.

إذا كانت ، بعد تغيير الأوعية ، متوازنة ، فإن إحدى العملات المعدنية الثلاثة التي تمت إزالتها من الميزان بعلامة زائد تكون أثقل من العملات الأخرى. يحتاج عالم الرياضيات إلى مقارنة اثنين منهم. إذا كانت متساوية ، والثالث مزيف. مع عدم المساواة ، الأثقل ليس حقيقيًا.

أومأ الإمبراطور برأسه مستحسناً وهو يستمع إلى المنطق رياضيات، ولكن الحاكم المخادع يذهب إلى السجن.

هذا اللغز هو ترجمة لفيديو TED-Ed.